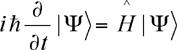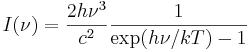Las ecuaciones matemáticas que cambiaron el mundo.
En el lenguaje de las matemáticas, las ecuaciones son como la poesía establecen verdades únicas y lo hacen con gran precisión, compactan grandes volúmenes de información en términos mas bien breves y, por lo general, son difíciles de entender por alguien no iniciado. Y así como la poesía nos ayuda a ver profundamente en nuestro interior, las matemáticas nos ayudan a ver mas allá de nosotros mismos; si a diferencia de la poesía con las matemáticas no podemos bajar el cielo, por lo menos sí podremos comprenderlo.
Comenzaremos definiendo una ecuación matemática. Una ecuación matemática es una expresión basada en números y letras, que permiten relacionar el comportamiento de cierto evento o fenómeno natural(aplicación física) o bien igualar algún concepto abstracto(aplicación matemática) con una entidad conocida. A lo largo de la historia, han existido una gran cantidad de desarrollos matemáticos, unos totalmente predecibles desde el punto de vista intuitivo(por lo tanto no requirieron mucho razonamiento) y otros desarrollos, fruto de una gran inspiración y entre estos existen algunos desarrollos que cuesta creer, como alguien pudo haber llegado hasta ahí, han sido verdaderas inspiraciones divinas, de estos últimos hablaremos en este post.
El teorema de Pitágoras
Es posible que Pitágoras fuese el primer matemático y filósofo del mundo occidental. Su obra cambió la visión contemporánea del mundo y en su muy conocido teorema establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Con él teorema de pitágoras se puede descubrir la longitud de un lado de un triángulo rectángulo, de la medida de sus otros dos lados. Pitágoras lo definió como: “La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa”. Por ejemplo: a ² + b ² = c ². En cualquier triángulo rectángulo se aplica esta regla. El teorema de pitágoras es la relación matemática más conocida y ofrece un importante valor práctico, teórico y didáctico, tanto en su versión aritmético-algebraica como en su versión geométrica.
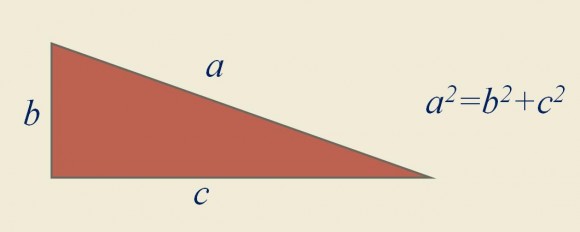
Por eso el teorema de pitágoras es una de las ecuaciones que cambiaron al mundo.
Principio de Arquimides
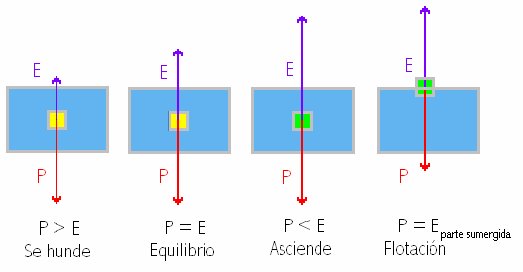
El principio de Arquímedes es un principio físico que afirma que: «Un cuerpo total o parcialmente sumergido en un fluido en reposo, recibe un empuje de abajo hacia arriba igual al peso del volumen del fluido que desaloja». Esta fuerza recibe el nombre de empuje hidrostático o de Arquímedes, y se mide en Newtons (en el SI). El principio de Arquímedes se formula así:
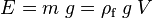
Donde E es el empuje, ρf es la densidad del fluido, V el «volumen de fluido desplazado» por algún cuerpo sumergido parcial o totalmente en el mismo, g la aceleración de la gravedad y m la masa.
Teorema Fundamental del Calculo
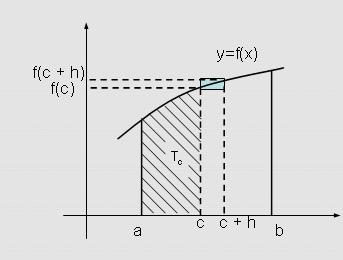
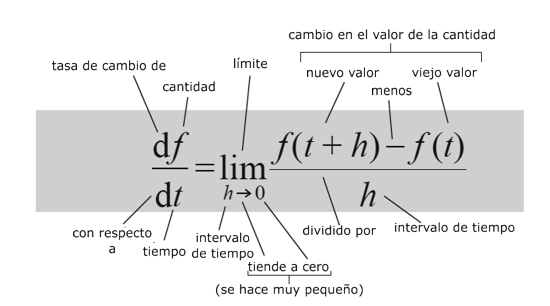
El calculo es una parte de las matemáticas que es mas dinámica, se trabaja principalmente con la idea de integrales o anti-derivadas, las cuales surgen del concepto básico del calculo que son los limites; Los limites extienden la imaginación en proceso matemático y dan soporte a las ideas fundamentales del calculo (diferencial e integral), sin los cuales la percepción de las matemáticas en el mundo actual no seria del impacto que tienen hoy en día.
Segunda ley de Newton y La ley de gravitación universal
Esta ley demostraba el enorme poder de las matemáticas para encontrar patrones escondidos en la naturaleza. Con un par de ecuaciones describió y predijo el movimiento de los planetas. Newton descubrió que se pueden resumir hechos e informacion de la naturaleza en un par de ecuaciones, y que el universo es predecible, aunque posteriormente su teoría fue superada por la teoría de la relatividad de Einstein, todavía es fundamental para casi todos los propósitos prácticos.
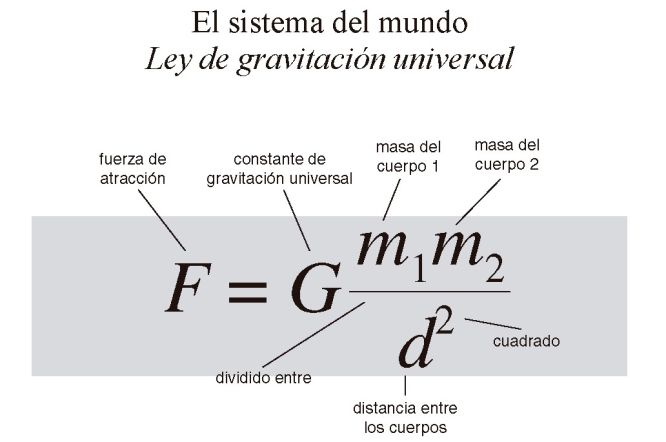
"El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime" - con lo cual podemos medir la fuerza.
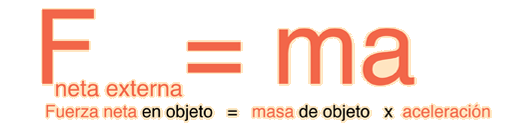
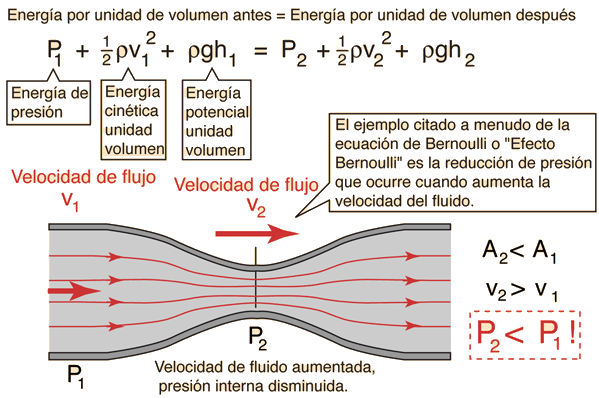
Ecuación de bernulli de fluidos
La ecuación de Bernoulli, se puede considerar como una apropiada declaración del principio de la conservación de la energía, para el flujo de fluidos. El comportamiento cualitativo que normalmente evocamos con el término "efecto de Bernoulli", es el descenso de la presión del líquido en las regiones donde la velocidad del flujo es mayor. En el flujo de alta velocidad a través de un estrechamiento, se debe incrementar la energía cinética, a expensas de la energía de presión. Dicho de otra forma la velocidad del agua se incrementa en proporción directa al estrechamiento. Por ejemplo, por un cuello de botella que fuera la mitad de ancho que el río normal, el agua pasara al doble de velocidad. Por un cuello de botella la tercera parte de ancho, el agua se movía tres veces más rápida que lo normal, y así sucesivamente.
Otro ejemplo seria el suponer el arca de Noé, las parejas de animales entraran por la puerta principal tocándose hombro con hombro. Supongamos que después de que Noé anotara su llegada en una gigantesca antecámara, tuvieran que meterse por un pasillo interior de uno en uno (el cuello de botella del arca) para llegar a sus establos; digamos que la puerta interior sería entonces la mitad de ancha que la puerta principal. Para que las cosas se mantuvieran en movimiento, todos los animales deberían duplicar su velocidad de paso por el cuello de botella del arca. Supongamos, por ejemplo, que los animales entraran en el arca a razón de una pareja por segundo… es decir, dos animales por segundo. Cuando cada pareja se dividiera para ir en fila india a los establos, todos los individuos deberían acelerar su paso, para poder pasar por el cuello de botella en medio segundo… dos veces más deprisa; de no hacerlo así, la ordenada procesión de animales se atascaría.
La aplicación en la fórmula de arriba se limita a los casos de flujo constante.
Teoría de la relatividad de Einstein
La teoría de la relatividad pretendía resolver la incompatibilidad existente entre la mecánica newtoniana y el electromagnetismo. La teoría de la relatividad general, publicada en 1915, es una teoría de la gravedad que reemplaza a la gravedad newtoniana, aunque coincide numéricamente con ella para campos gravitatorios débiles y "pequeñas" velocidades. La teoría general se reduce a la teoría especial en ausencia de campos gravitatorios.
Los cambios predichos por Einstein sólo son notables a grandes velocidades. Tales velocidades han sido observadas entre las partículas subatómicas, viéndose que los cambios predichos por el genial científico se daban realmente, y con gran exactitud. Es más, sí la teoría de la relatividad de Einstein fuese incorrecta, los aceleradores de partículas no podrían funcionar, las bombas atómicas no explotarían y habría ciertas observaciones astronómicas imposibles de hacer.
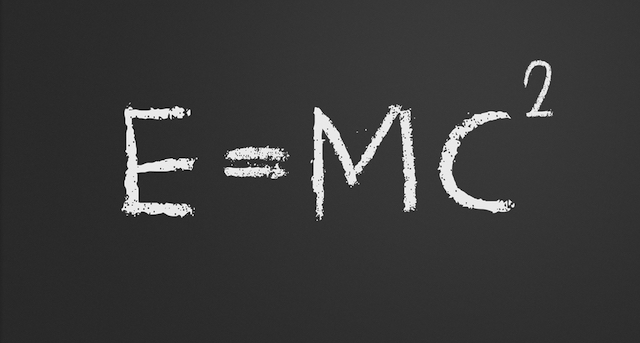
Formula de Euler
Una de las formulas mas bellas en el mundo de las matemáticas, porque involucra números claves, para las mismas, e, pi, i, 1 y 0.

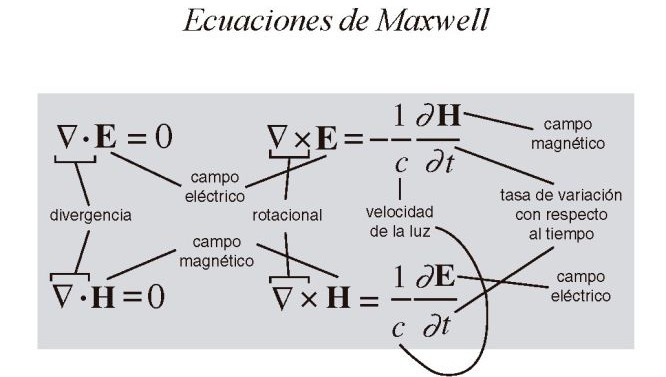
Ecuaciones de Maxwell
Las ecuaciones de Maxwell representan una de las formas mas elegantes y concisas de establecer los fundamentos de la Electricidad y el Magnetismo. Aunque fue Faraday quien descubrió la relación entre electrizad y magnetismo, fue realmente Maxwell quien propuso las ecuaciones fundamentales del electromagnetismo. Las ecuaciones de maxwell tuvieron una tremenda repercusión en el desarrollo tecnológico del siglo XX( televisión, radio, radar, teléfono).
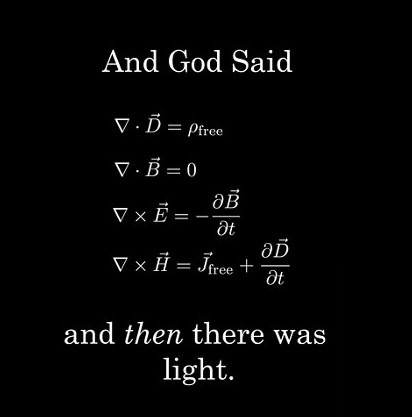
Distribución normal
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales. La distribución de probabilidad conocida como distribución normal es, por la cantidad de fenómenos que explica, las mas importantes de las distribuciones estadísticas.
La distribución normal fue presentada por primera vez por Abraham de Moivre en 1738, Laplace uso la distribución normal en el análisis de errores de experimentos, el método de mínimos cuadrados fue introducido por Legendre en 1805. Gauss que afirmaba haber usado el método normal desde 1794, lo justificó rigurosamente en 1809 asumiendo una distribución normal de los errores. EL nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos.
El nombre de "campana" viene de Espirit Jouffret que usó el termino "bell surface" (superficie campana) por primera vez en 1872 para una distribución normal bivariante de componentes independientes. El nombre de "distribución normal" fue otorgado independientemente por Charles S., Francis Galton y Wilhelm Lexis hacia 1875.
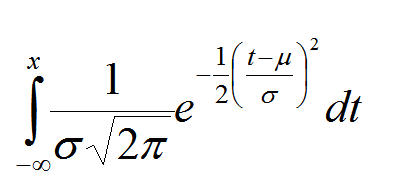
Fórmula de Euler para los poliedros
Nos presenta el inicio y desarrollo de una de las ramas de la matemática pura, la topología. Aunque afirma que la mayoría de las aplicaciones son indirectas, destaca que nos ayuda a comprender el funcionamiento de la molécula de la vida: el ADN.
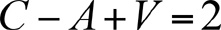
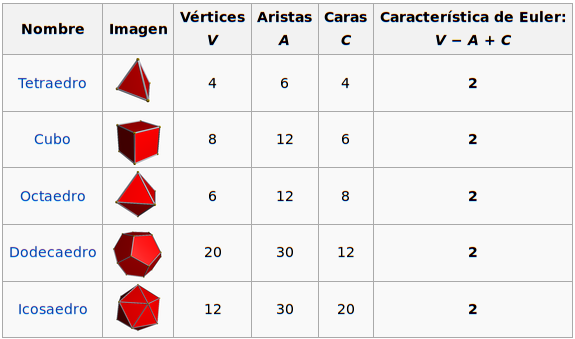
Este es un resultado muy interesante y visualmente sorprendente. Considere un poliedro P no importa si este es regular o irregular. La fórmula de Euler indica que si C representa el número de caras del poliedro, A representa el número de aristas y V representa el número de vértices del poliedro entonces se cumple que C + V - A = 2
Por ejemplo si tomamos un cubo cualquiera este tendrá seis caras, ocho vértices y doce aristas. En este caso C= 6, V=8, A=12 de donde fácilmente vemos que C+V-A= 6+8-12=2
Segunda ley de la termodinámica
Segunda ley de la termodinámica. A partir de la importancia de la máquina de vapor en el desarrollo industrial surge la necesidad de mejorar su rendimiento. Los conceptos de calor, temperatura, entro-pía. Permite poner límites al trabajo útil que puede extraerse a partir del calor.
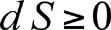
Ecuaciones de Plank
La ley de Planck describe la radiación electromagnética emitida por un cuerpo negro en equilibrio térmico en una temperatura definida. O dicho de otra manera ¿Porque emite luz un objeto cuando se calienta?.
Establece las proporciones de energía que emite un cuerpo a cierta temperatura, en distintos colores —distintas longitudes de onda— del espectro.
La ecuación de Black-Scholes.
La teoría de la valoración de opciones fue revolucionada con la publicación del trabajo de Fisher Black y Myron Scholes (1973) en el que presentaron su conocida fórmula para la determinación del valor teórico de una opción. Durante las décadas siguientes el problema de la valoración de opciones ha ocupado la mayor parte del tiempo de los investigadores en el campo de las finanzas. Más recientemente, las técnicas y modelos de valoración de opciones desarrollados muchos de ellos a partir del sugerente modelo Black-Scholes rebajando alguno de sus supuestos simplificadores, han sido aplicados a una gran variedad de situaciones que van más allá del simple mercado de opciones.
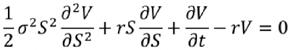
Sin duda uno de los modelos matemáticos más influyentes en grandes decisiones financieras a nivel mundial.
Teoría del caos
La teoría del caos, tiene innumerables aplicaciones en toda la ciencia, incluyendo el movimiento de los planetas del Sistema Solar, la predicción del tiempo, la dinámica de poblaciones en ecología, las estrellas variables, el modelado de terremotos y trayectorias eficientes para las sondas espaciales.
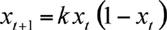
La ecuación de onda.
Vivimos en un mundo de ondas. Nuestras orejas detectan ondas de compresión en el aire, llamamos a esto «oído». Nuestros ojos detectan ondas de radiación electromagnética, llamamos a esto «vista». Cuando un terremoto azota un pueblo o una ciudad, la destrucción la causan ondas en el cuerpo sólido de la Tierra. Cuando un barco se balancea en el océano, está reaccionando a las ondas en el agua. Los surfistas usan las ondas del mar como diversión; la radio, la televisión y gran parte de las redes de teléfonos móviles usan las ondas de la radiación electromagnética, similares a las que vemos, pero de longitudes de onda diferentes. Los microondas... bueno, el nombre lo dice todo, ¿no?
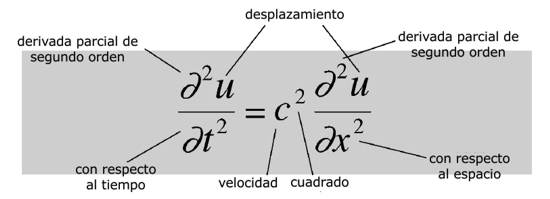
La aceleración de un pequeño segmento de la cuerda de un violín es proporcional al desplazamiento medio de los segmentos vecinos.
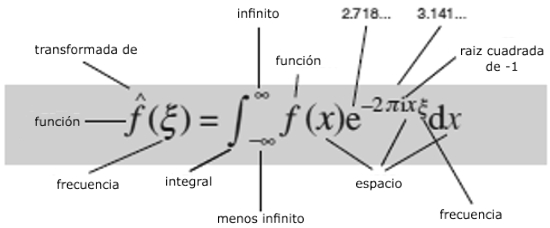
La transformada de Fourier.
La técnica de Fourier se usa muchísimo, por ejemplo, en tratamiento de imágenes y mecánica cuántica. Se usa para encontrar la estructura de moléculas biológicas grandes como el ADN, para comprimir datos de imágenes en fotografía digital, para limpiar grabaciones de audio viejas o dañadas y para analizar terremotos. Variantes modernas se usan para almacenar datos de huellas digitales de manera eficiente y mejorar escáneres médicos.
Ecuación de Dirac.
La naturaleza está mucho más loca de lo que pensamos: las partículas pueden estar en estados sin posiciones o energía definidas, pueden estar en estados donde coexisten posibilidades que en nuestra escala son mutuamente excluyentes, etc.
“Si dos sistemas interactúan uno con el otro durante un cierto período de tiempo y luego se separan, lo podemos describir como dos sistemas separados, pero de alguna manera sutil están convertidos en un solo sistema. Uno de ellos sigue influyendo en el otro, a pesar de kilómetros de distancia o años luz”. Esto es el entrelazamiento cuántico o conexión cuántica. Dos partículas que, en algún momento estuvieron unidas, siguen estando de algún modo relacionadas. No importa la distancia entre ambas, aunque se hallen en extremos opuestos del universo. La conexión entre ellas es instantánea.”
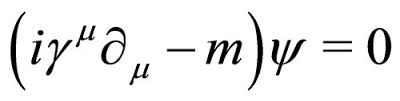
Una de las aplicaciones de esta ecuación es que es posible encontrar tumores gracias a la anti-materia.
Ecuación de Schrödinger.
Es la ecuación definitiva de la mecánica cuántica, es posiblemente la teoría mas exacta y mas potente jamas concebida por la humanidad. Fue ésta la ecuación que revolucionaria la tecnología, permitiendo el desarrollo de los rayos láser, discos compactos, ordenadores y dispositivos de comunicación.
La luz tenía comportamientos de onda y de materia. Pero no solamente la luz sino toda la materia. Esta ecuación modela la materia no como una partícula sino como una onda y describe el modo de propagación de estas ondas. Es fundamental para la mecánica cuántica que rige el mundo de lo muy pequeño. Y se analizan conclusiones, muy difíciles de entender, que se deducen de esta ecuación.